Blog

An Importance Sampling Method for arbitrary BRDFs used in Global Illumination Applications 读书总结

Posted on Edited on In

An Importance Sampling Method for arbitrary BRDFs used in Global Illumination Applications

一种全局照明应用中任意BRDFs的重要采样方法

Abstract 摘要

全局照明算法应用：

  • 现代电影的特效
  • 室内灯光设计
  • 电子游戏

真实感图像渲染

  • 数值计算模拟光的传播[Mil84, WRC88, GSCH93, GTGB84, CWH93]
  • 全局照明算法[wh80, CPC84, Kaj86, WH92]
  • 提高蒙特卡洛方法[VG94, Sbe96, Vea97, BSW00, ARBJ03,BGH05, JTE05, CJAMJ05, CETC06]

本文主要内容：

  1. 全局照明反射模型的最新技术
  2. 一个适合全局照明系统的场景编辑器，自研图形格式：GRF
  3. BRDF 编辑器
  4. 一般BRDFs的有效采样
  5. 有效的光照采样和BRDF产品功能

第一章 Introduce 简介

1.1Realistic Image Synthesis 真实感图形生成

全局照明是计算机图形学的一个领域，它的目标是产生真实的图像，展示光与真实物体相互作用时产生的大部分效果。这是一个主要目标，但目前这个目标是有限的，因为模仿自然从来不是一项简单的任务。必须考虑以下几个方面:

  • 几何模型的构建
  • 纹理和透明度的应用
  • 照明和阴影技术
  • 使用硬件技术实现实时可视化

光照和阴影模型来计算表面上每一点的强度和颜色。

有两类照明算法:

  • Local Illumination methods (LI) 局部照明方法
  • Global Illumination method (GI) 全局照明方法

它们之间的关系取决于物体之间是否有相互反射。

场景中呈现的物体的外观、亮度和颜色将取决于：

  • 表面特性:色彩、透明度、反射率等。
  • 观察者在现场的位置。
  • 照明条件，如光源的强度、几何形状和位置，
  • 环境和大气条件(雾、烟等)。

阴影计算的核心集中在模拟光与物体的复杂相互作用。在现实意义上是复杂的，数以百万计的相互反射发生，因此很难完全模拟它们。为了简化这一过程，我们使用了理想漫反射面和理想镜面等理论情况。

1.2 The dual nature of light 光的波粒二象性

The Propagation of Light 光的传播

可见光，波长从400到700纳米不等。

700纳米以上的波长是肉眼不可见的，它们对应于所谓的红外光。在400纳米以下的光叫做紫外线。

对应的电磁辐射频率 \(3.84 \times 10^{14}\)到\(7.69 \times 10^{14} \mathrm{~Hz}\)

Interaction of Light and Matter 光与物质的相互作用

光照和着色模型需要考虑光与物质的相互作用，需要考虑折射和反射。

1.3 Representation of Surfaces 曲面的球面表示

描述物体表面反射行为的方法是双向反射分布函数(BRDF)。这个数学函数是双向的，因为它取决于两个方向，一个指向观察者，另一个指向光源。

通过这种方式，BRDF或反射率模型描述了反射光的颜色和分布。选择特定的模型和参数使我们能够模拟特定类型的材料，因此它是真实图像生成的重要组成部分。

第二章 Reflectance models in Global Illumination 全局光照的反射模型

2.1 A Light Model for Global Illumination 全局光照的灯光模型

Mathematical Notation 数学符号

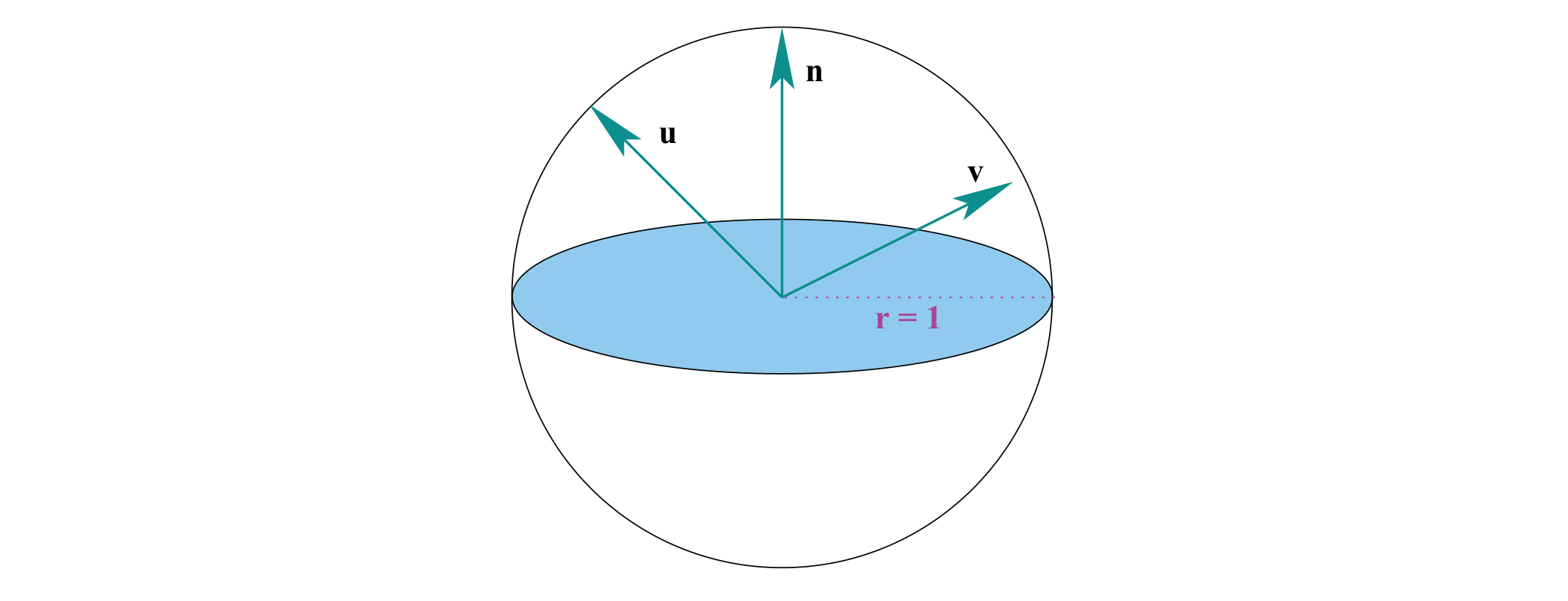
  • \(\mathcal{S}^{2}\)域是所有标准化方向的集合。XY平面把球体分成两个相等的半球。

  • surface normal 表面法线 定义为z轴方向的单位向量

\[ \mathbf{n} \stackrel{\text { def }}{=}(0.0 .1) \]

  • 正面半球定义 Omegasub

\[ \Omega \stackrel{\text { def }}{=} \quad\left\{\mathbf{v} \in \mathcal{S}^{2} \mid \mathbf{v} \cdot \mathbf{n}>0\right\} \]

  • 反面半球定义

\[ \mho \stackrel{\text { def }}{=}\left\{\mathbf{v} \in \mathcal{S}^{2} \mid \mathbf{v} \cdot \mathbf{n} \leq 0\right\} \]

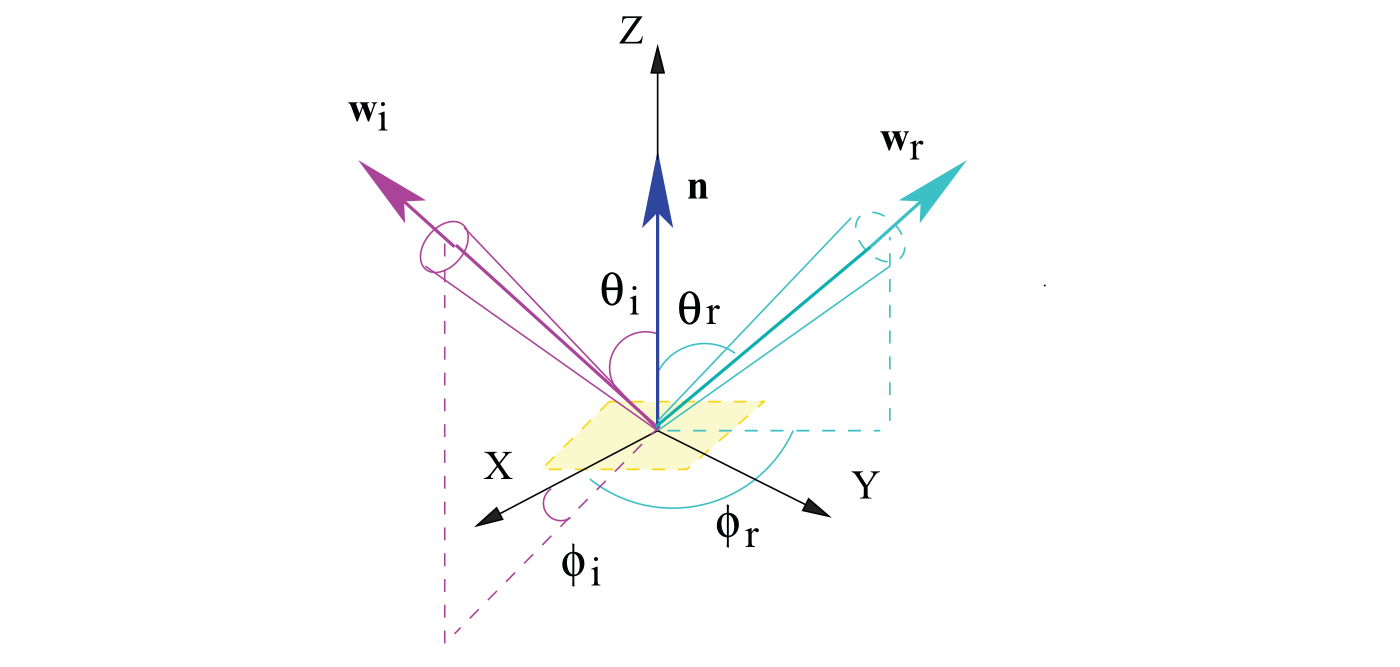
  • 在局部坐标系中入射向量和反射向量
  • 极角 polar angle \(\theta_{\mathbf{u}}\) 向量和Z轴之间的夹角
  • 方位角 azimuthal angle \(\phi_{\mathbf{u}}\) 在平面XY上关于X轴的投影
  • 极坐标和笛卡尔坐标的转换

\[ \begin{array}{l} x_{\mathbf{u}}=\cos \left(\phi_{\mathbf{u}}\right) * \sin \left(\theta_{\mathbf{u}}\right), \\ y_{\mathbf{u}}=\sin \left(\phi_{\mathbf{u}}\right) * \sin \left(\theta_{\mathbf{u}}\right), \\ z_{\mathbf{u}}=\cos \left(\theta_{\mathbf{u}}\right) \end{array} \]

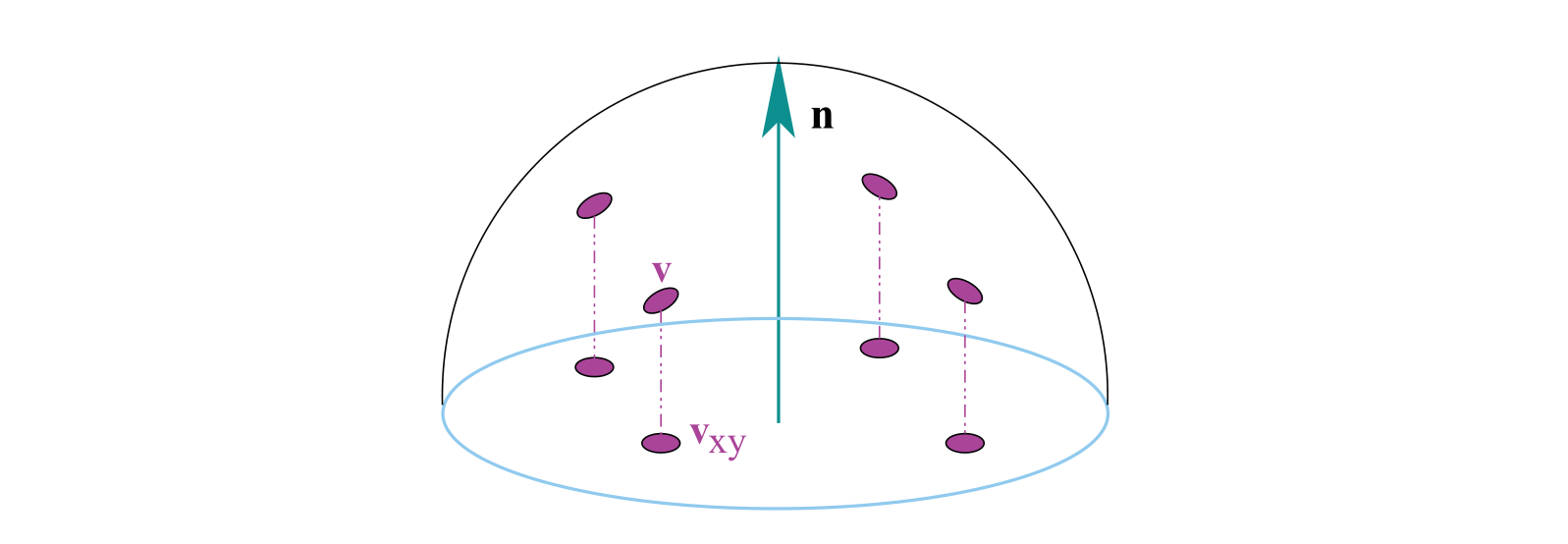
  • 二维平面集合定义

\[ \mathbf{v}_{x y} \in \mathcal{D}^{2} \]

\[ \mathcal{D}^{2} \stackrel{\text { def }}{=} \quad\left\{(x, y) \in E^{2} \text { t.q. } x^{2}+y^{2}<1\right\} \]

  • 映射函数 \(h:\Omega \rightarrow \mathcal{D}^{2}\) 映射半球面到二维平面

\[ h(\mathbf{v})=h\left(x_{\mathbf{v}}, y_{\mathbf{v}}, z_{\mathbf{v}}\right) \stackrel{\text { def }}{=}\left(x_{\mathbf{v}}, y_{\mathbf{v}}\right)=\mathbf{v}_{x y} \]

  • h的反函数 （根据二维平面的点返回半球面坐标）

\[ \mathbf{v}=h^{-1}\left(\mathbf{v}_{x y}\right)=h^{-1}\left(x_{\mathbf{v}}, y_{\mathbf{v}}\right)=\left(x_{\mathbf{v}}, y_{\mathbf{v}}, z_{\mathbf{v}}\right) \mid z_{\mathbf{v}}=\sqrt{1-x_{\mathbf{v}}^{2}-y_{\mathbf{v}}^{2}} \]

  • steradian 球面度 符号: $$

    球面度的微分公式

\[ d \sigma(\mathbf{v}) \stackrel{\text { def }}{=} \frac{d A\left(\theta_{\mathbf{v}}, \phi_{\mathbf{v}}\right)}{r^{2}}=\frac{\left(r d \theta_{\mathbf{v}}\right)\left(r \sin \left(\theta_{\mathbf{v}}\right) d\left(\phi_{\mathbf{v}}\right)\right)}{r^{2}}=\sin \left(\theta_{\mathbf{v}}\right) d\left(\theta_{\mathbf{v}}\right) d\left(\phi_{\mathbf{v}}\right) \]

  • 对任意向量 \(\mathbf{v} \in \Omega\)定义立体投影角\(\sigma_{p}\)为:

\[ d \sigma_{p}(\mathbf{v}) \stackrel{\text { def }}{=}(\mathbf{v} \cdot \mathbf{n}) d \sigma(\mathbf{v}) \]

  • area measure 度量面积 $ d A(x, y)$

\[ \begin{array}{c} d A\left(\mathbf{u}_{x y}\right)=d A\left(x_{\mathbf{u}}, y_{\mathbf{u}}\right)=d x d y=d \sigma_{p}\left(h^{-1}\left(x_{\mathbf{u}}, y_{\mathbf{u}}\right)\right) \\ d \sigma_{p}(\mathbf{u})=d A(h(\mathbf{u}))=d A\left(\mathbf{u}_{x y}\right) \end{array} \]

Radiant Flux Density 辐射通量密度

基础物理量

物理量 符号 国际单位制 注释
辐射出射度（Radiant exitance） Me 瓦特每平方米 表面出射的辐射通量
辐射度（Radiosity） Je or Jeλ 瓦特每平方米 表面出射及反射的辐射通量总和
辐射率（Radiance） Le 瓦特每球面度每平方米 每单位立体角每单位投射表面的辐射通量。
辐射能（Radiant energy） Qe 焦耳 能量。
辐射能量密度（Radiant energy density） ωe 焦耳每立方米
辐射强度（Radiant intensity） Ie 瓦特每球面度 每单位立体角的辐射通量。
辐射曝光量（Radiant exposure） He 焦耳每平方米
辐射通量（Radiant flux） Φe 瓦特 每单位时间的辐射能量，亦作“辐射功率”。
辐照度（Irradiance） Ee 瓦特每平方米 入射表面的辐射通量。
光谱辐射出射度（Spectral radiant emittance） Meλ 或 Meν 瓦特每立方米 或 瓦特每平方米每赫兹 表面出射的辐射通量的波长或频率的分布
光谱辐射率（Spectral radiance） Leλ 或 Leν 瓦特每球面度每立方米 或 瓦特每球面度每平方米每赫兹 常用W⋅sr−1⋅m−2⋅nm−1
光谱辐照度（Spectral irradiance） Eλ 或 Eν 瓦特每立方米 或 瓦特每平方米每赫兹 通常测量单位为 W·m−2·nm−1
光谱功率（Spectral power） Φeλ 瓦特每米 辐射通量的波长分布
光谱强度（Spectral intensity） Ieλ 瓦特每球面度每米 辐射强度的波长分布
  • 辐射通量密度是每个单位区域在表面上的辐射通量。辐射通量密度以每平方米瓦特（Wm）为单位进行测量

能量（Energy）

能量是所有辐射学中单位的起点，它的单位是焦耳（J）。光源不断地向外发射光子，每一个光子都处在特定的波长上并且携带一定数量的能量。一个波长为\(\lambda\)的光子所携带的能量为： \[ Q=\frac{h c}{\lambda} \] 式子中 \(h\) 和 \(c\) 为物理学中的两个常量, 其中 \(c\) 为光速, \(c \approx 299,472,458 m / s, h\) 为 普朗克常量, \(h \approx 6.626 \times 10^{-34} \mathrm{~m}^{2} \cdot \mathrm{kg} / \mathrm{s}\) 。

通量（Flux）

能量是物理系统在一定时间内做功本领的度量。在处理渲染问题时，基于稳态假设，我们通常是在一个很短的时间跨度上对光进行度量。

辐射通量（Radiant flux），又称功率（Power），是单位时间内通过某一个表面或者区域的能量的总和。辐射通量可以通过计算能量与时间的微商得到 \[ \Phi=\lim _{\Delta t \rightarrow 0} \frac{\Delta Q}{\Delta t}=\frac{d Q}{d t} \] 辐射通量的单位是焦耳每秒 \((J / s)\) 或者瓦特 \((W)\), 前者是后者的定义，而后者更加常用。

离开物体(考虑表面区域)的功率是由物体发出的\(\Phi_{e}\)的功率和从入射通量\(\Phi_{i}\)反射的部分\(\Phi_{r}\)的能量所产生的。 \[ \Phi=\Phi_{e}+\Phi_{r} \] 注意，我们也可以称透射通量为\(\Phi_{t}\)。

辐照度与辐射出射度（Irradiance and Radiant Exitance）

  • 给定有限面元 \(A\), 可以定义出该面元上功率关于面积的密度 \(\frac{\Phi}{A}\) 。这样的一个物理量在表示到 达物体表面的平均功率密度时叫做辐照度 (irradiance)，此时用 \(E\) 表示;

  • 在表示离开物体表面 的平均功率密度时叫做辐射出射度（radiant exitance)，此时用 \(M\) 表示。辐照度和辐射出射度 的单位是瓦特每平方米 \(\left(W / m^{2}\right)\) 。

  • 表面出射的辐射通量，用M 或者 exitance表示：

\[ M(x)=\frac{d \Phi(x)}{d A(x)} \]

  • 入射表面的辐射通量，用E 或者 irradiancia 表示：

\[ E(x)=\frac{d \Phi_{i}(x)}{d A(x)} \]

  • 离开表面的能量是自身发出的能量和反射的能量的总和：

\[ M(x)=M_{e}(x)+M_{r}(x)=\frac{d \Phi_{e}(x)}{d A(x)}+\frac{d \Phi_{r}(x)}{d A(x)} \]

The Radiance Function 辐射率函数

辐射率（Radiance） ：每单位立体角每单位投射表面的辐射通量。

辐射率函数 ：计算给定目标点和目标方向的光照亮度 \[ d L_{r}(x, \mathbf{u})=\frac{d^{2} \Phi(x, \mathbf{u})}{d A_{p}(x) d \sigma(\mathbf{u})}=\frac{d^{2} \Phi(x, \mathbf{u})}{\cos (\mathbf{u}) d A(x) d \sigma(\mathbf{u})}=\frac{d^{2} \Phi(x, \mathbf{u})}{d A(x) d \sigma_{p}(\mathbf{u})} . \] 单位： \[ W \cdot m^{-2} \cdot s r^{-1} \]

同时可以得出入射方向的辐射率计算公式： \[ d L_{i}(x, \mathbf{v})=\frac{d\left(d \Phi_{i}(x, \mathbf{v})\right)}{d A(x) \cos (\mathbf{v}) d \sigma(\mathbf{v})}=\frac{d E(x, \mathbf{v})}{d \sigma_{p}(\mathbf{v})} \]

\[ d E(x, \mathbf{v})=d L_{i}(x, \mathbf{v}) \cos (\mathbf{v}) d \sigma(\mathbf{v}) \]

如果我们对所有的立体角的辐射进行积分，我们就得到了单位时间单位面积内到达或离开表面的能量。出射度与辐照度的积分形式为: \[ \begin{aligned} M_{r}(x) &=\int_{\Omega} d L_{r}(x, \mathbf{u}) d \sigma_{p}(\mathbf{u}) \\ E(x) &=\int_{\Omega} d L_{i}(x, \mathbf{v}) d \sigma_{p}(\mathbf{v}) \end{aligned} \]

2.2 Dispersion of Light in a Surface 光在表面上的散射

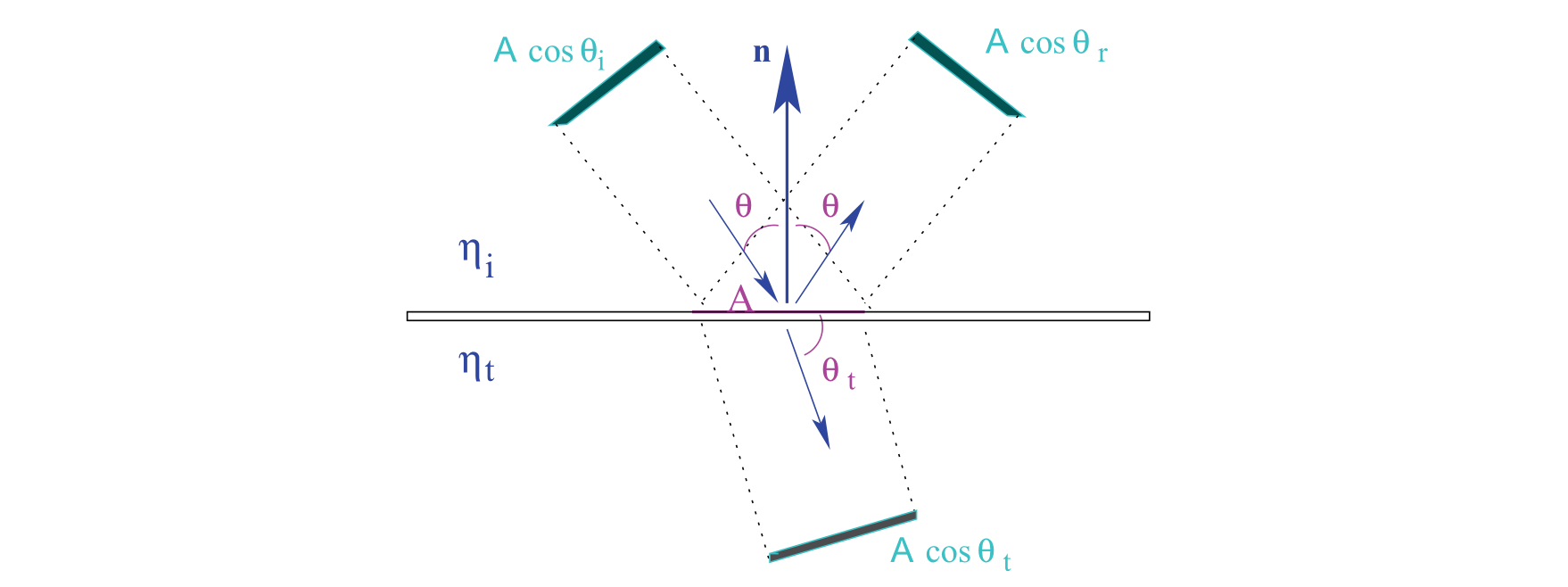
image-20210418225811774

  • 当光通过不同的介质时，一部分在介质上反射，另一部分在改变其方向后传播。

  • 透射、反射和折射现象是微观事件的宏观表现。

  • 使用的规则是基本的能量守恒: 如果我们知道两种介质的折射率，就有可能计算出它所传递的能量。

\[ \Phi_{i} A \cos \left(\theta_{i}\right)=\Phi_{r} A \cos \left(\theta_{r}\right)+\Phi_{t} A \cos \left(\theta_{i}\right) \]

The Law of Reflection 反射定律

  • 反射现象使我们能够看到不发光的物体。
  • 物体根据其表面以不同的方式反射。
  • 反射光线的表面以不同的方式产生光。
  • 反射光只向一个方向发出，称为理想镜面反射。
  • 反射光向各个方向发散，称为理想漫反射。

反射定律:

  1. 镜面的入射、反射和法向量在同一平面上。
  2. 入射角和反射角相同。

给定入射方向计算反射方向：

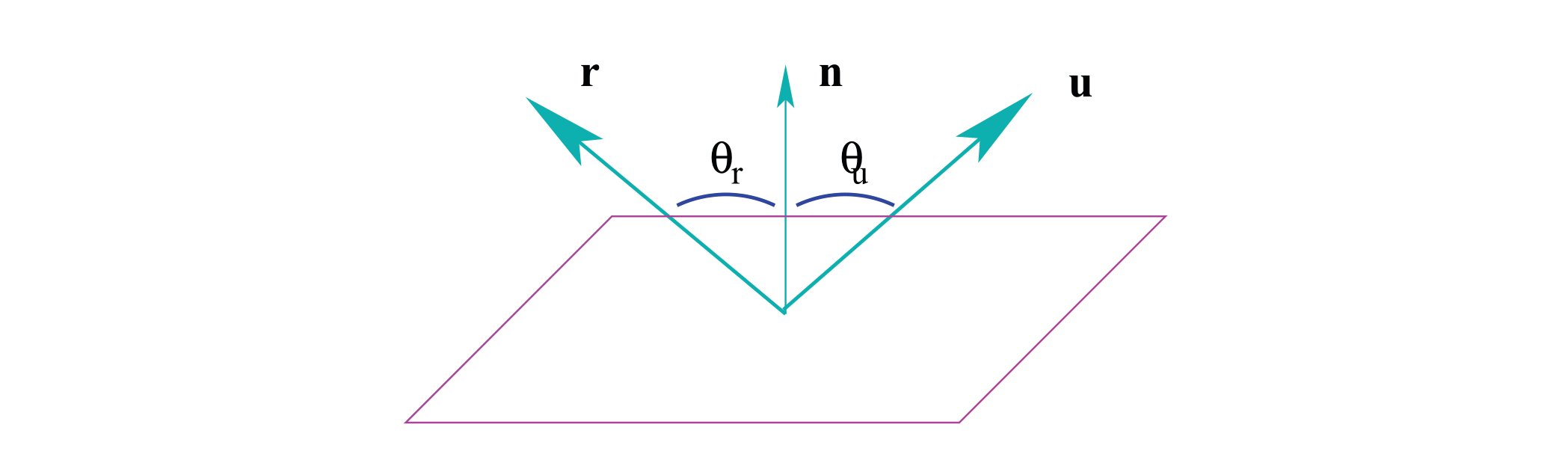\[ \begin{array}{l} \theta_{r}=\theta_{u} \\ \phi_{r}=\phi_{u} \pm \pi, \\ \mathbf{r}=\mathbf{u}-2(\mathbf{u} \cdot \mathbf{n}) \mathbf{n} . \end{array} \]

The Law of Refraction 折射定律

  • 当一束光撞击两种密度(波速)不同的透明介质之间的界面时，光在传输过程中发生折射。
  • 光线方向由于入射角和介质的折射率的关系，会发生偏移。
  • 全反射现象：对于一个给定的入射角，折射角是\(99^{\circ}\)。这种现象叫做全反射。

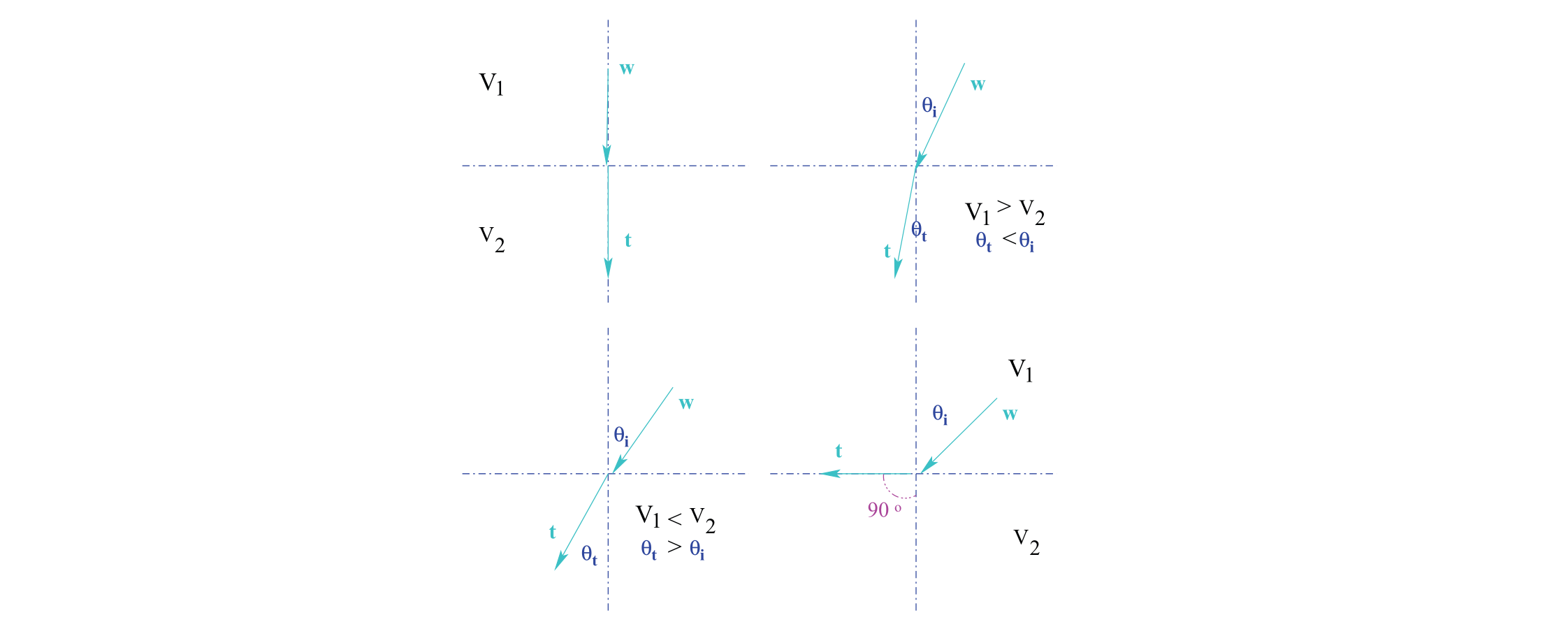
  • 第一行，当一束光进入光学密度较大的介质，即具有较大折射率的介质时，光会向垂线方向弯曲。

  • 第二行，当光束从密度较高的介质流向密度较低的介质时，它会偏离垂线。

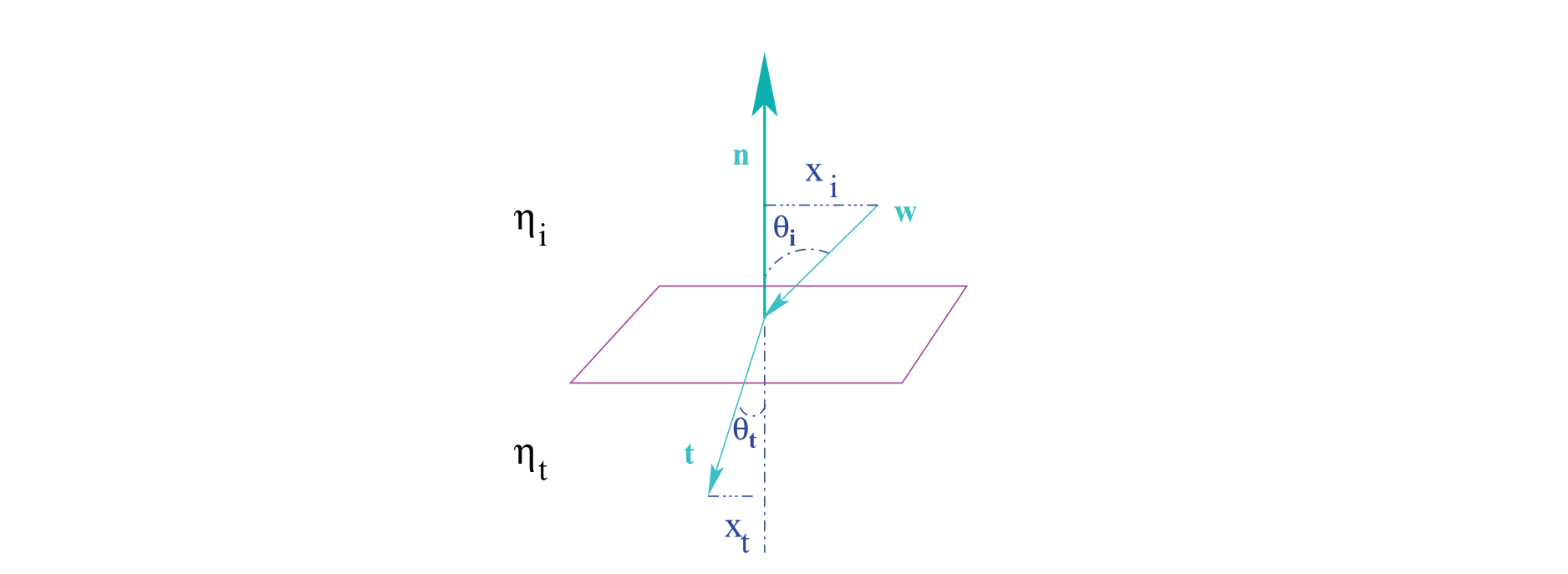
  • 入射角与反射角之差的关系是一个定值，用来定义折射率\(\eta=x_{i} / x_{t}\)

菲涅尔定律

1621年，Willebrord Snell阐明了折射现象的定律:

  • 入射、反射和折射的光线都在入射平面内
  • \(\eta_{i} \sin \theta_{i}=\eta_{t} \sin \theta_{t}\)

The Bidirectional Scattering Distribution Function 双向反射分布函数

  • 真实的物体不是纯粹的反射性或纯粹的传递性。
  • BSDF or BTDF（双向散射分布函数），是描述散射光的物理行为的数学函数。

\[ \operatorname{BRDF} f_{r}: \Omega_{i} \times \Omega_{r} \longrightarrow \mathbb{R} \]

\[ \text { BTDF } f_{t}: \Omega_{i} \times \Omega_{t} \longrightarrow \mathbb{R} \]

  • 单位：\(s r^{-1}\)

2.3 The Local Reflection of Light 光的局部反射

The Bidirectional Reflectance Distribution Function 双向反射分布函数

  • 双向反射率分布函数，是曲面反射率的参数表示。
  • 这个函数表示光与物质的相互作用，通过将来自v方向的辐射与离开物体的u方向的辐射联系起来。这是下面关系的常数值:

\[ d L_{r}(x, \mathbf{u}) \propto d E_{i}(x, \mathbf{v}) \]

BRDF是6个参数的函数，但为了降低其复杂度和维数，通常需要进行一些简化。

如果假设：

  • 反射率的分布不随表面变化。没有必要把公式中隐含的点x表示出来。
  • 光立即反射，因此没有必要直接表达时间变量。这样的简化是不可能模拟磷光现象的。
  • 射出的光束与入射的光束有相同的波长λ，即相同的频率ν -;我们忽略了荧光现象。
  • 将亮度参数和BRDF、λ简化为三个不同的颜色(RGB)值带。波长隐含在公式中。

则： \[ f_{r}(\mathbf{u}, \mathbf{v}) \in[0, \infty) \] 等价于： \[ f_{r}\left(\theta_{\mathbf{u}}, \phi_{\mathbf{u}}, \theta_{\mathbf{v}}, \phi_{\mathbf{v}}\right) \] 公式： \[ f_{r}(\mathbf{u}, \mathbf{v})=\frac{d L_{r}(\mathbf{u})}{d E_{i}(\mathbf{v})}=\frac{d L_{r}(\mathbf{u})}{L_{i}(\mathbf{v}) d \sigma_{p}(\mathbf{v})} \]

BRDF属性：

  • Symmetry 对称性

    它必须服从Helmholz Reciprocity Rule，这是光的物理结果，表明BRDF是相对于u和v对称的。

\[ f_{r}(\mathbf{u}, \mathbf{v})=f_{r}(\mathbf{v}, \mathbf{u}) \quad \forall \mathbf{u}, \mathbf{v} \in \Omega \]

  • Energy Conservation Law 能量守恒定律

    入射辐射不能能在任何一点上完全被反射

\[ \int_{\Omega} f_{r}(\mathbf{u}, \mathbf{v}) d \sigma_{p}(\mathbf{v})<1 \quad \forall \mathbf{u} \in \Omega \]

BRDF 局部坐标系的一种替代方法：

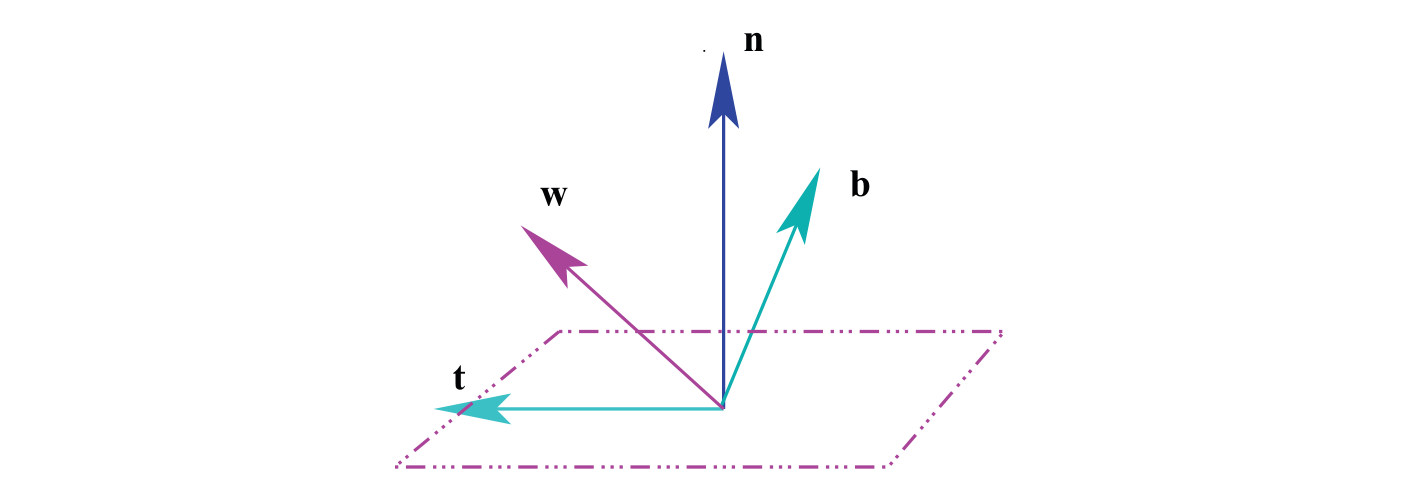\[ \begin{array}{l} \mathbf{b} \stackrel{\text { def }}{=}(\mathbf{w} \times \mathbf{t}) \\ \cos \left(\theta_{\mathbf{w}}\right) \stackrel{\text { def }}{=}(\mathbf{n} \cdot \mathbf{w}), \\ \tan \left(\phi_{\mathbf{w}}\right) \stackrel{\text { def }}{=} \frac{(\mathbf{b} \cdot \mathbf{w})}{(\mathbf{t} \cdot \mathbf{w})} \end{array} \]

  • 副法向量b
  • 切向量t

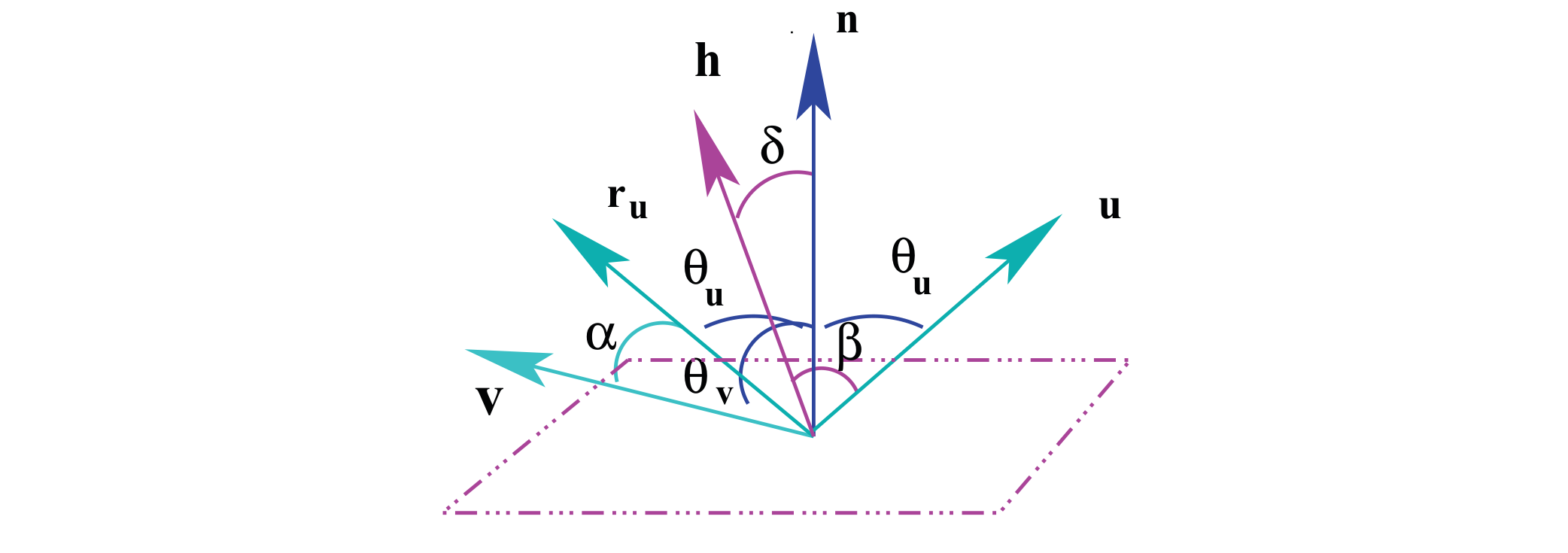\[ \forall \mathbf{u}, \mathbf{v}, \mathbf{n} \in \Omega\left\{\begin{array}{l} \alpha \stackrel{\text { def }}{=} \cos ^{-1}\left(\mathbf{r}_{\mathbf{u}} \cdot \mathbf{v}\right), \\ \beta \stackrel{\text { def }}{=} \cos ^{-1}(\mathbf{u} \cdot \mathbf{h}), \\ \delta \stackrel{\text { def }}{=} \cos ^{-1}(\mathbf{h} \cdot \mathbf{n}), \\ \mathbf{h} \stackrel{\text { def }}{=} \frac{\mathbf{u}+\mathbf{v}}{\|\mathbf{u}+\mathbf{v}\|} . \end{array}\right. \]

halfway vector 半角向量

通常用来计算高光，这种方法避免了反射向量的显式计算，并且易于实现。

BRDF 分类:

  • Approximated 近似性

    主要目的是提供一个简单的公式，专门设计来模拟一种反射。因此，一个快速的计算模型，可由参数调整，而不背后的物理基础。例如Phong和Blinn-Phong。

  • Theoretical 理论性

    这些模型试图近似真实的光色散现象。它们需要更多的计算工作，这有时会区分它们，它们通常不被用于渲染系统。例如Cook-Torrance。每个理论模型都局限于特定类型的材料。

  • Experimental 实验性

    有时理论模型并不那么实用。这就是为什么有些模型通过测量数据来模拟真实现象的原因。BRDF可以通过光度仪获得，手动或机械地改变光源和传感器。这一过程可能需要数小时，因此其他技术使用数码相机在一张照片上获取许多BRDF样本。该方法给出的公式也可以通过参数进行调整，但不同之处在于它们是用来调整测量数据的。

对物质的分类：

  • Isotropic BRDFs 各向同性

    代表一种材料，其反射不取决于表面的方向，通常是粗糙的。可以简化BRDF参数：

\[ f_{r}\left(\theta_{i}, \theta_{r}, \phi_{r}-\phi_{i}\right) \]

\[ \forall \alpha \in[0,2 \pi], \alpha>0 \Longrightarrow f_{r}\left(\theta_{r}, \phi_{r}, \theta_{i}, \phi_{i}\right)=f_{r}\left(\theta_{r}, \phi_{r}+\alpha, \theta_{i}, \phi_{i}+\alpha\right) \]

  • Anisotropic BRDFs 同向异性

    即使矢量u和v是固定的，当表面以n为角α旋转时，光的反射也会不同。这种材料给条纹外观看到的是拉丝金属效果。

Representations for the BRDF 表示BRDF

  • 复杂和精细的BRDFs经常考虑到入射和出射角、波长、偏振、位置和时间。

  • 对于计算机图形学来说，有许多变量，因此这会导致冗长的计算。更简单的BRDFs在计算光传输时考虑了射线光学而不是波动光学。

  • 射线光学把光看作不相互作用的直线射线，每一条射线都携带一定的能量。射线光学通过忽略波长简化了方程的符号和表达式。

  • 由于忽略了波长，因此也忽略了光波相互作用所产生的干涉、衍射和偏振的影响。

  • 传统上，计算机图形系统要么依赖于分析模型，要么必须存储大量数据来表示，即使是简单的BRDFs。

  • 最简单的BRDF表示将BRDF的样本存储在一个规则的四维网格上，并在它们之间进行插值。采用这种方法，插值后的数据容易产生噪声，结果不理想。此外，在掠射角附近通常会有缺失的数据点。

  • 除这些问题外，存储一个完整的BRDF，可能需要很多兆字节。

  • 鉴于BRDFs的大小和高维，许多技术已经开发出来，以有效地存储和计算它们：

    例如:拟合数据到一个解析模型，使用样条贴片，球面谐波基函数，球面小波和泽尼克多项式。使用前面提到的技术之一来更改变量可以获得更有效的表示方法。使用球谐波来表示BRDF是另一种方法。正弦和余弦的球形类似物，位于频域中。信号的每一部分都被称为基函数，所有基函数的和可以精确地再现原始信号。因为可能需要无数个基函数来精确地重现所需的BRDF，通常只使用这些基函数的子集。使用太少的基函数会导致视觉上的错误，使用太多的基函数在计算上非常昂贵。

  • BRDF的因式分解是一种成本较低的方法，可以准确地表示BRDF，也适用于蒙特卡罗渲染系统中的采样。

The Surface Reflectance 表面反射率的测定

  • （reflectance function）反射函数\(\rho\)或反射率（albedo）决定了反射能量与入射能量的比值。

  • 它接受0到1之间的值，并且没有单位。

  • BRDF表现为方向依赖性，反照率只是一个比值。

  • 在一个点的反射率计算使用BRDF对给定方向的积分:

\[ \rho(\mathbf{u}) \stackrel{\text { def }}{=} \int_{\Omega} f_{r}(\mathbf{u}, \mathbf{v}) \cos (\mathbf{v}) d \sigma(\mathbf{v}) . \]

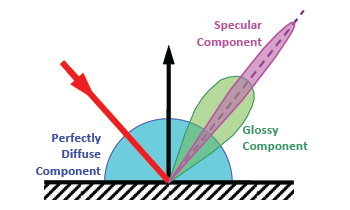
光散射现象可以分为三个部分：

  • 均匀漫反射

  • 方向漫反射

  • 镜面反射

  • 镜面反射是一种适用于镜面的现象。它的特征是镜面反射率\(\rho_{s}(\mathbf{u}) \in[0,1)\)，依赖于入射角和菲涅耳系数。

  • 均匀漫反射\(\rho_{d} \in[0,1)\)，或兰伯特分量（Lambertian component），不依赖于入射方向，在每个方向上都相等地反射光。这是一种理想的现象，因为没有纯粹的漫反射材料。

  • 方向漫反射分量，可以考虑不同类型的反射率。

    设\(\rho_{h d}(x, \mathbf{u})\)为半球方向的反射率，即半球上光照在给定方向上的反射率。

\[ \rho_{h d}(x, \mathbf{u})=\frac{L_{r}(x, \mathbf{u})}{E(x)}=\int_{\Omega} f_{r}(x, \mathbf{u}, \mathbf{v}) d \sigma_{p}(\mathbf{u}) . \]

  • 与方向漫反射分量相关的倒数是方向半球反射率(directional-hemispherical reflectance)，即整个反射半球的积分。

    这两个函数是相同的\(\rho_{h d}=\rho_{d h}\)，因此我们使用唯一的符号\(\rho\)。

\[ \rho_{d h}(x, \mathbf{v})=\frac{d E_{r}(x, \mathbf{v})}{d E_{i}(x)}=\int_{\Omega} f_{r}(x, \mathbf{u}, \mathbf{v}) d \sigma_{p}(\mathbf{v}) \]

The Fresnel Equations 菲涅耳方程

  • 当光照射到一个表面并发生反射或透射时，我们不仅需要知道光的新方向，我们还需要知道被反射或传递的能量的比例: 反射率 (reflectivity) R和透射率 (transmittance) T;

  • 它们是用麦克斯韦方程组求解的。在 polished surfaces 的情况下，这些方程被称为菲涅耳方程。

  • 有两种类型发方程：

    • 对于本质上不含锰的介质材料，例如晶体

    • 对于电导体，例如金属。在任何一种情况下，光的偏振都被考虑，并且两个系数与反射和透射现象相关。

菲涅尔方程： \[ \begin{array}{c} L_{r}=F L_{i} \\ L_{t}=T\left(\frac{\eta_{t}}{\eta_{i}}\right)^{2} L_{i} \end{array} \]

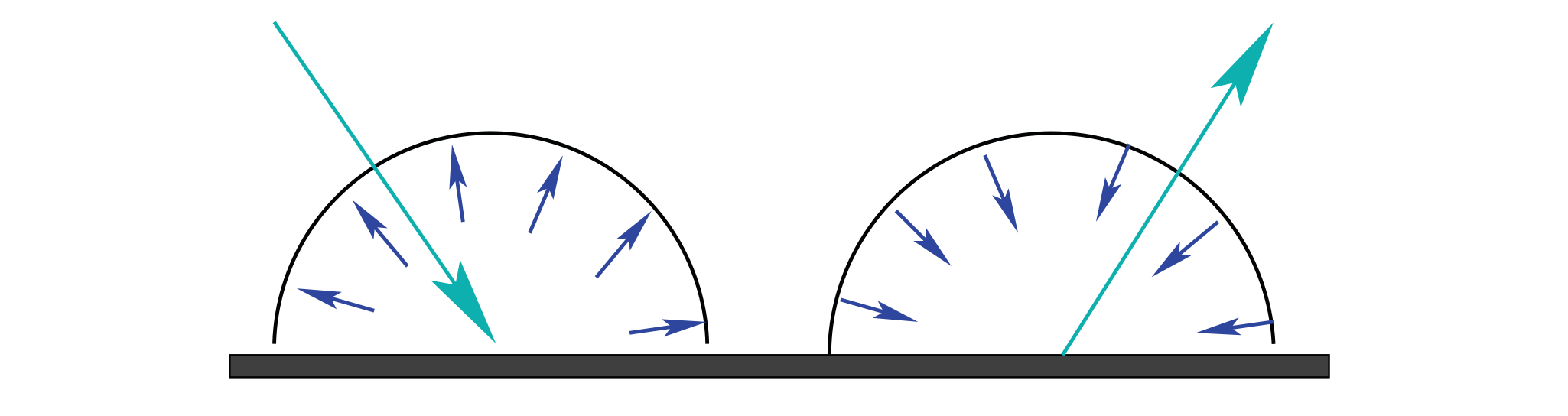
方向-半球形反射率 (directional-hemispherical) 和半球形-方向反射率 (hemispherical-directional) 相同。

2.4 The Radiance Equation

是Kajiya首先提出，用二阶Fredholm积分来表示光传输方程(LTE)。

光传输方程描述了均衡的辐射分布：\(L_{i}(x, \mathbf{v})=L_{r}\left(y, \mathbf{u}^{\prime}\right)\) , y是最近的交点

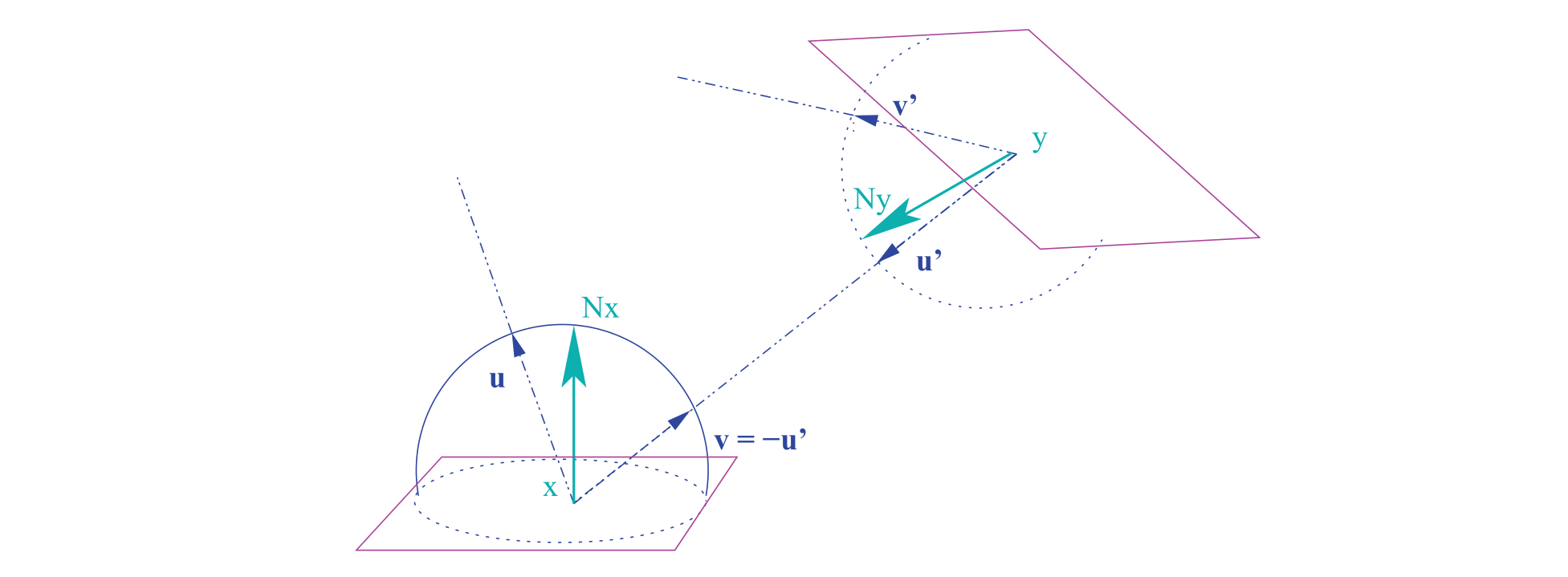
光线离开点y到达点x。

\[ \begin{aligned} L_{r}(\mathbf{u}) & \stackrel{\text { def }}{=} \int_{\Omega} d L_{r}(\mathbf{u}) d \sigma(\mathbf{v}) \\ &=\int_{\Omega} f_{r}(\mathbf{u}, \mathbf{v}) L_{i}(\mathbf{v})(\mathbf{v} \cdot \mathbf{n}) d \sigma(\mathbf{v}) . \end{aligned} \] 使用投射立体角测量的辐射方程的最终表达式 \[ \begin{aligned} L(\mathbf{u}) &=L_{e}(\mathbf{u})+L_{r}(\mathbf{u}) \\ &=L_{e}(\mathbf{u})+\int_{\Omega} f_{r}(\mathbf{u}, \mathbf{v}) L_{i}(\mathbf{v}) d \sigma_{p}(\mathbf{v}) . \end{aligned} \]

第三章 BRDF模型的研究

着色模型并不总是考虑现实(或物理)，通常认为眼睛看不见的东西不需要计算。

3.1 Ideal Specular Reflection (1621) 理想的镜面反射

理想的镜面反射遵循反射定律，向单一方向反射，除反射方向r外，其他方向总是为零。: \(L_{r, s}(x, \mathbf{u})=L_{i}\left(x, \mathbf{r}_{\mathbf{u}}\right)\)

方程： \[ f_{r, s}(\mathbf{u}, \mathbf{v})=\rho_{s}(\mathbf{v}) \delta_{\mathbf{u}}(\mathbf{v}) \]

\[ \delta_{\mathbf{u}}(\mathbf{v}) \stackrel{\text { def }}{=}\left\{\begin{array}{ll} 1 & i f \mathbf{v}=\mathbf{r}_{\mathbf{u}} \\ 0 & \text { else. } \end{array}\right. \]

  • \(\rho_{s}\)为该点的镜面反射率

3.2 Lambert (1760)

第一个反射率模型是由Minnaert提出的，他想要模拟月球表面反射率。这不仅可以应用到月球上，也可以应用到我们会看到边缘变暗的物体上。该模型由两个参数\(\rho_{d}\)和一个负责使目标变暗的指数控制。该BRDF的解析表达式为： \[ f_{r}(\mathbf{u}, \mathbf{v})=\frac{\rho_{d}}{\pi}(\cos (\mathbf{u}) \cos (\mathbf{v}))^{k-1} \]

当k = 1时，这个函数等价于lambertian函数。

3.4 Torrance-Sparrow (1967)

  • 这是一个考虑偏振光的物理模型，用于粗糙表面。
  • 表面粗糙度采用v形等长凹陷，称为microfacet 微平面。
  • 它们的方向是随机的，并由参数控制，因此可以模拟不同程度的粗糙度。

完整的BRDF函数如下: \[ f_{r}(\mathbf{u}, \mathbf{v})=\frac{k_{d}}{\pi}+\frac{k_{s}}{4 \pi(\mathbf{n} \cdot \mathbf{v})} D(\mathbf{h}) F\left(\theta_{\mathbf{u}}\right) G(\mathbf{u}, \mathbf{v}) \]

  • microfacets distribution 微平面描述函数 \(D: \Omega \rightarrow \mathbb{R}\) , \(D(\mathbf{h}) \in[0,1]\)

    给出了相对于h矢量排列的平面的法线分布，并由m对其进行了描述，

    Beckmann分布:

\[ D(\mathbf{h})=\frac{1}{m^{2} \cos (\delta)^{4}} \exp \left(\frac{\cos (\delta)^{2}-1}{m^{2} \cos (\delta)^{2}}\right) \]

  • Fresnel factor 菲涅尔系数 \(F\left(\theta_{\mathbf{u}}\right) \in[0,1]\) 给出在每个microfacet上反射的光的比例。其计算的是菲涅尔方程的各极化态系数的线性组合

垂直光偏振系数 \[ r_{\perp}(\theta)=\frac{a^{2}+b^{2}-2 a \cos (\theta)+\cos ^{2}(\theta)}{a^{2}+b^{2}+2 a \cos (\theta)+\cos ^{2}(\theta)} \]

\[ \begin{array}{c} 2 a^{2}=\sqrt{\left(\eta^{2}-\kappa^{2}-\sin ^{2}(\theta)\right)^{2}+4 \eta^{2} \kappa^{4}}+\left(\eta^{2}-\kappa^{2}-\sin ^{2}(\theta)\right) \\ 2 b^{2}=\sqrt{\left(\eta^{2}-\kappa^{2}-\sin ^{2}(\theta)\right)^{2}+4 \eta^{2} \kappa^{4}}\left(\eta^{2}-\kappa^{2}-\sin ^{2}(\theta)\right) \end{array} \]

平行光偏振系数 \[ r_{\|}(\theta)=r_{\perp}(\theta) \frac{a^{2}+b^{2}-2 a \sin (\theta) \tan (\theta)+\sin ^{2}(\theta) \tan ^{2}(\theta)}{a^{2}+b^{2}+2 a \sin (\theta) \tan (\theta)+\sin ^{2}(\theta) \tan ^{2}(\theta)} \]

  • Geometric attenuation factor 几何衰减因子 \(G(\mathbf{u}, \mathbf{v}) \in[0,1]\)

表面由于掩蔽或阴影遮挡，光的一部分不会到达目的地

\[ G(\mathbf{u}, \mathbf{v})=\min \left\{1, \frac{2(\mathbf{n} \cdot \mathbf{h})(\mathbf{n} \cdot \mathbf{u})}{(\mathbf{u} \cdot \mathbf{h})}, \frac{2(\mathbf{n} \cdot \mathbf{h})(\mathbf{n} \cdot \mathbf{v})}{(\mathbf{u} \cdot \mathbf{h})}\right\} \]

Torrance-Sparrow BRDF 是各向同性材料最完整的物理反射模型之一

3.5 Beard-Maxwell (1973)

Beard-Maxwell BRDF是一种基于物理特性的经验模型，它模拟了一种特定类型的材料，油漆表面。反射主要由表面反射和体积反射两部分组成。

  • superficial \(f_{r, \text { sup }}\)

    表面反射是发生在表面第一层的镜面反射。这一层由microfacet表示，其法线方向遵循统计分布D。

  • volumetric \(f_{r, v o l}\)

体积反射分量是由地下水平面的光散射引起的。它主要由两个作用产生:第一层的局部镜面反射(其法线为n)和内部层的光反射的体积反射近似。

\[ f_{r \lambda}(\mathbf{u}, \mathbf{v})=f_{r, s u p \lambda}(\mathbf{u}, \mathbf{v})+f_{r, v o l} \lambda(\mathbf{u}, \mathbf{v}) \]

表面反射分量由介质的菲涅耳系数控制 (使用k = 0 y η = 1,65)，计算公式为: \[ f_{r, s u p}(\mathbf{u}, \mathbf{v})=-\frac{F(\beta)}{F(0)} \frac{f_{r}(\mathbf{h}) \cos ^{2}(\mathbf{h})}{\cos (\mathbf{u}) \cos (\mathbf{v})} S O(\mathbf{u}, \mathbf{h}, \tau, \Omega) \]

//TODO:

3.6 Phong (1975)

Phong 是一个非常流行的BRDF模型，它是第一个描述non-lambertian表面的模型。

它既不服从能量守恒也不服从相互作用的经验模型，但它的简单性使它成为计算机图形学中最常用的模型之一。

本质上，这个模型是对Torrance & Sparrow的简化，其中G和F因子被降低

D简化为: \[ D(\mathbf{u}, \mathbf{v})=\cos ^{n}(\alpha)=\left(\mathbf{u} \cdot \mathbf{r}_{\mathbf{v}}\right)^{n} \]

  • 参数\(n\) :\(n \in[0, \infty]\) 用来控制镜面反射

此外，通过对指数算子的优化，该模型可以更快，如Schlick给出的: \[ \cos ^{n}(\alpha) \approx \frac{\cos (\alpha)}{n-n \cos (\alpha)+\cos (\alpha)} . \] 第二个和第三个参数是镜面反射系数\(k_{s}\)和漫反射系数\(k_{d}\)，均取[0,1] \[ f_{r}(\mathbf{u}, \mathbf{v})=k_{d}(\mathbf{v} \cdot \mathbf{n})+k_{s}(\mathbf{u} \cdot \mathbf{r})^{n} \]

3.7 Blinn (1977)

通过法向量和半角向量获取高光 \[ D(\mathbf{h})=(\mathbf{n} \cdot \mathbf{h})=\cos (\delta) \]

\[ f_{r}(\mathbf{u}, \mathbf{v})=k_{d}(\mathbf{u} \cdot \mathbf{n})+k_{s}(\mathbf{n} \cdot \mathbf{h})^{n} \quad \text { with } k_{d}+k_{s}=1 \]

3.8 Cook-Torrance (1981)

  • 现实中所发生的反射现象既不是纯粹的漫反射面也不是纯粹的镜面，所以线性组合它们并不是最好的选择。
  • Cook和Torrance使用光学理论寻找解决方案，他们使用了以前的著作以及一些新想法:只有那些面向h矢量的microfacet才有助于最终的反射。
  • 该模型还在渲染领域引入了一种新型材料，区分了金属和非金属表面。
  • 反射是用三个组成部分来描述的:环境部分，漫射部分和镜面部分。

\[ \rho=\rho_{a}+k_{s} \rho_{s}+k_{d} \rho_{d}, \quad \text { donde } k_{s}+k_{d}<1 \]

高斯分布 \[ D(\mathbf{h})=\cos (\beta) e^{-\left(\frac{\alpha}{m}\right)^{2}} \] Beckman 分布 \[ D(\mathbf{h})=\frac{1}{m^{2} \cos ^{4}(\alpha)} e^{-\left[\frac{\tan (\alpha)}{m}\right]^{2}} \]

高光计算 \[ f_{r, s}(\mathbf{u}, \mathbf{v})=\frac{F(\beta)}{\pi} \frac{D(\mathbf{h}) G(\mathbf{u}, \mathbf{v})}{(\mathbf{n} \cdot \mathbf{u})(\mathbf{n} \cdot \mathbf{v})} \]

//TODO:

3.9 Kajiya (1985)

Kajiya模型[Kaj85]实现了蛮力的各向异性方法，估计了反射强度光的解析形式。它是基于Kirchoff近似和一个平稳的基础方法来近似辐射方程(Eq. 2.12)。Kajiya考虑了一个简化的粗糙表面模型，并在其位置上使用了最近的切面。

在这项工作中，Kajiya计算和存储反射率在一个表每次表面照明评估。之后，使用表中的值进行线性插值。尽管他使用了一种新的数字t

3.10 Poulin-Fournier (1990)

3.11 Strauss (1990)

3.12 He-Torrance-Sillion-Greenberg (1991)

3.13 Ward (1992)

3.14 Westin (1992)

3.15 Lewis (1993)

3.16 Schlick (1993)

3.17 Hanrahan (1993)

3.18 Oren-Nayar (1994)

3.19 Neumann-Neumann (1996)

3.20 Lafortune (1997)

3.21 Shirley (1997)

3.22 Ashikhmin-Shirley (2000)

3.23 Granier-Hiedrich (2003)

第四章 Sampling of the BRDF BRDF采样

论文记录

visual human system [Gla94, Bue01]

Law of Reflection [FvDaSFH90]

Helmholz Reciprocity Rule [CP85]

[PF90, KM99] 局部坐标计算BRDF

We consider the following classification given by Ward [War92]: BRDF 分类？

其他相关文章

Radiant Flux Density (Irradiance and Radiant Exitance)

Radiance wiki